Tutorial¶
Introduction¶
A time series is a sequence of observations, or data points, that is arranged based on the times of their occurrence. The hourly measurement of wind speeds in meteorology, the minute by minute recording of electrical activity along the scalp in electroencephalography, and the weekly changes of stock prices in finances are just some examples of time series, among many others. Some of the following properties may be observed in time series data [gutsequential]:
- the data is not generated independently
- their dispersion varies in time
- they are often governed by a trend and/or have cyclic components
The study and analysis of time series can have multiple ends: to gain a better understanding of the mechanism generating the data, to predict future outcomes and behaviors, to classify and characterize events, or more.
In [2]:
ts_anim()
Out[2]:
In time-domain astronomy, data gathered from the telescopes is usually represented in the form of light-curves which are time series that show the brightness variation of an object through a period of time (for a visual representation see video below). Based on the variability characteristics of the light-curves, celestial objects can be classified into different groups (quasars, long period variables, eclipsing binaries, etc.) and consequently can be studied in depth independently.
Classification of data into groups can be performed in several ways given light curve data: primarily, existing methods found in the literature use machine learning algorithms that group light-curves into categories through feature extraction from the light-curve data. These light-curve features, the topic of this work, are numerical or categorical properties of the light-curves which can be used to characterize and distinguish the different variability classes. Features can range from basic statistical properties such as the mean or the standard deviation to more complex time series characteristics such as the autocorrelation function. These features should ideally be informative and discriminative, thus allowing for machine learning or other algorithms to use them to distinguish between classes of light-curves.
In this document, which allows for the fast and efficient calculation of a compilation of many existing light-curve features. The main goal is to create a collaborative and open tool where users can characterize or analyze an astronomical photometric database while also contributing to the library by adding new features. However, it is important to highlight that this library is not necessarily restricted to the astronomical domain and can also be applied to any kind of time series data.
Our vision is to be capable of analyzing and comparing light curves from any available astronomical catalog in a standard and universal way. This would facilitate and make more efficient tasks such as modeling, classification, data cleaning, outlier detection, and data analysis in general. Consequently, when studying light curves, astronomers and data analysts using our library would be able to compare and match different features in a standardized way. In order to achieve this goal, the library should be run and features generated for every existent survey (MACHO, EROS, OGLE, Catalina, Pan-STARRS, VVV, etc.), as well as for future surveys (LSST), and the results shared openly, as is this library.
In the remainder of this document, we provide an overview of the features developed so far and explain how users can contribute to the library. A Readme file is also available in case of needing extra information.
Video 1: Light-Curve of Triple Star¶
The video below shows how data from the brightness intensity of a star through time results on a light-curve. In this particular case we are observing a complex triple system in which three stars have mutual eclipses as each of the stars gets behind or in front of the others.
In [3]:
macho_video()
Out[3]:
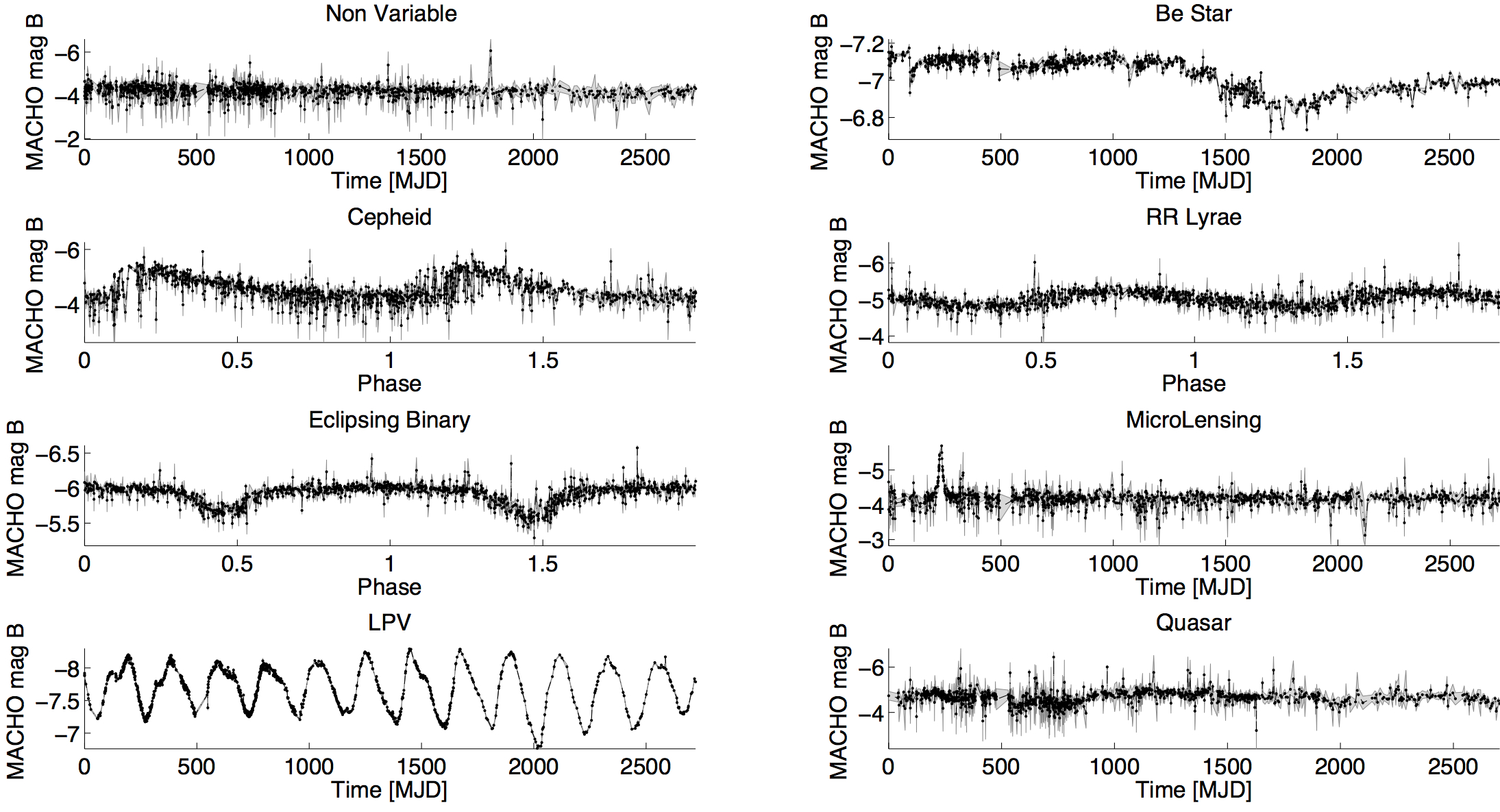
The following figure presents example light-curves of each class in the MACHO survey. The x-axis is the modified Julian Date (MJD), and the y-axis is the MACHO B-magnitude.
In [4]:
macho_example11()
Out[4]:
Library structure¶
The library is coded in python and can be downloaded from the Github repository https://github.com/carpyncho/feets. New features may be added by issuing pull requests via the Github version control system. For a quick guide on how to use github visit https://guides.github.com/activities/hello-world/.
It is also possible to obtain the library by downloading the python package from https://pypi.python.org/pypi/feets or by directly installing it from the terminal as follows:
$ pip install feets
The library receives as input the time series data and returns as output an array with the calculated features. Depending on the available input the user can calculate different features. For example, if the user has only the vectors magnitude and time, just the features that need this data will be able to be computed.
In order to calculate all the possible features the following vectors (also termed as raw data) are needed per light curve:
- time
- magnitude
- error
- magnitude2
- time2
- error2
where 2 refers to a different observation band. It is worth pointing out that the magnitude vector is the only input strictly required by the library given that it is necessary for the calculation of all the features. The remaining vectors are optional since they are needed just by some features. In other words, if the user does not have this additional data or he is analyzing time series other than light curves, it is still possible to calculate some of the features. More details are presented in the next section.
This is an example of how the input could look like if you have only magnitude and time as input vectors:
In [5]:
lc_example = np.array([time_ex, magnitude_ex])
lc_example
Out[5]:
array([[ 0.00000000e+00, 1.00000000e+00, 2.00000000e+00,
3.00000000e+00, 4.00000000e+00, 5.00000000e+00,
6.00000000e+00, 7.00000000e+00, 8.00000000e+00,
9.00000000e+00, 1.00000000e+01, 1.10000000e+01,
1.20000000e+01, 1.30000000e+01, 1.40000000e+01,
1.50000000e+01, 1.60000000e+01, 1.70000000e+01,
1.80000000e+01, 1.90000000e+01, 2.00000000e+01,
2.10000000e+01, 2.20000000e+01, 2.30000000e+01,
2.40000000e+01, 2.50000000e+01, 2.60000000e+01,
2.70000000e+01, 2.80000000e+01, 2.90000000e+01],
[ 3.17997948e-01, 3.48217914e-01, 9.08475451e-01,
6.51132985e-01, 2.97248304e-01, 1.54407114e-01,
5.12057284e-01, 5.16049151e-01, 9.09945692e-01,
1.89520143e-01, 4.53077218e-01, 5.87709814e-01,
2.09509012e-01, 8.99530602e-01, 7.77350784e-01,
3.73799849e-01, 5.28389700e-01, 8.61119159e-02,
9.95733391e-01, 7.68746004e-01, 1.98000961e-01,
5.27104265e-01, 7.26077963e-01, 6.16347034e-01,
7.25787884e-01, 9.63982369e-01, 9.03672853e-03,
3.82209587e-02, 2.09076940e-01, 9.62195846e-01]])
When observed in different bands, light curves of a same object are not always monitored for the same time length and at the same precise times. For some features, it is important to align the light curves and to only consider the simultaneous measurements from both bands. The aligned vectors refer to the arrays obtained by synchronizing the raw data.
Thus, the actual input needed by the library is an array containing the following vectors and in the following order:
- time
- magnitude
- error
- magnitude2
- aligned_time
- aligned_magnitude
- aligned_magnitude2
- aligned_error
- aligned_error2
The library structure is divided into two main parts.
- feets.FeatureSpace: is a wrapper class that allows the user to select the features to be calculated based on the available time series vectors or to specify a list of features.
- feets.extractors: A package containing the actual code for calculating the features, and multiple tools to create your own extractor. Each feature has its own extractor class and every extractor can create at leat one feature.
The following code is an example of a class in extractors package that calculates the slope of a linear fit to the light-curve:
import feets
from scipy import stats
class LinearTrend(feets.Extractor): # must inherit from Extractor
data = ['magnitude', 'time'] # Which data is needed
# to calculate this feature
features = ["LinearTrend"] # The names of the expected
# feature
# This method receives the data specified in the
# previous line with the same name
def fit(self, magnitude, time):
regression_slope = stats.linregress(time, magnitude)[0]
# The return value must be a dict with the same values
# defined in features
return {"LinearTrend": regression_slope}
If the user wants to use their features after the declaration of the
extractor they must register the class with the register function.
For example:
feets.register_extractor(LinearTrend)
Reading example light curve¶
Feets comes with a MACHO Example light-curve,with all the 9 parameters needed to calculate all the posible features.
In [6]:
from feets.datasets import macho
lc = macho.load_MACHO_example()
print("ID:", print(lc.id))
print("Bands:", lc.bands)
lc_1.3444.614
ID: None
Bands: ('R', 'B')
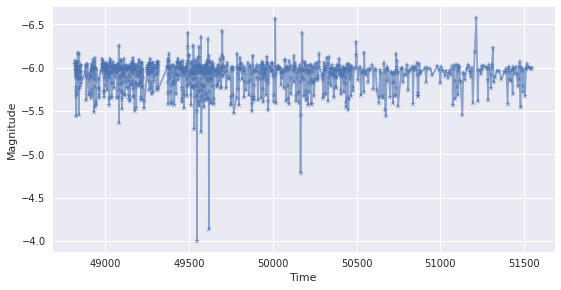
It is sometimes helpful to visualize the data before processing it. For a representation of the light curve, we can plot it as follows:
In [7]:
p = plt.plot(lc.data.B.time, lc.data.B.magnitude, '*-', alpha = 0.6)
plt.xlabel("Time")
plt.ylabel("Magnitude")
plt.gca().invert_yaxis()
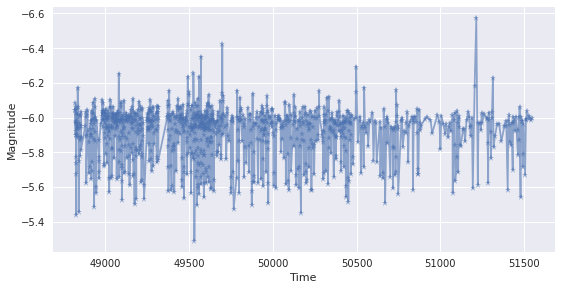
Preproccess¶
Besides opening the file, the data we noww need to:
- Remove noise: points within 5 standard deviations from the mean are considered as noise and thus are eliminated.
- Align: it synchronizes the light-curves in the two different
bands and returns
aligned_time,aligned_magnitude,aligned_magnitude2,aligned_errorandaligned_error2.
In [8]:
import feets.preprocess
# removing noise of the data
time, mag, error = feets.preprocess.remove_noise(**lc.data.B)
time2, mag2, error2 = feets.preprocess.remove_noise(**lc.data.R)
# We synchronize the data
atime, amag, amag2, aerror, aerror2 = feets.preprocess.align(
time, time2, mag, mag2, error, error2)
lc = [time, mag, error,
mag2, atime, amag, amag2,
aerror, aerror2]
plt.plot(lc[0], lc[1], '*-', alpha = 0.6)
plt.xlabel("Time")
plt.ylabel("Magnitude")
plt.gca().invert_yaxis()
Choosing the features¶
The library allows the user to either choose the specific features of interest to be calculated or to calculate them all simultaneously. Nevertheless, as already mentioned, the features are divided depending on the input data needed for their computation (magnitude, time, error, second data, etc.). If unspecified, this will be used as an automatic selection parameter. For example, if the user wants to calculate all the available features but only has the vectors magnitude and time, only the features that need magnitude and/or time as an input will be computed.
Note: some features depend on other features or must be computed
together. For instance, Period_fit returns the false alarm
probability of the estimated period. It is necessary then to calculate
also the period PeriodLS.
The list of all the possible features with their corresponding input data, additional parameters and literature source is presented in the following table:
In [9]:
features_table()
Out[9]:
| Feature | Computed with | Dependencies | Input Data |
|---|---|---|---|
| Amplitude | magnitude | ||
| AndersonDarling | magnitude | ||
| Autocor_length | magnitude | ||
| Beyond1Std | magnitude, error | ||
| CAR_mean | CAR_sigma, CAR_tau | magnitude, error, time | |
| CAR_sigma | CAR_mean, CAR_tau | magnitude, error, time | |
| CAR_tau | CAR_mean, CAR_sigma | magnitude, error, time | |
| Color | magnitude, magnitude2 | ||
| Con | magnitude | ||
| Eta_color | aligned_magnitude2, aligned_magnitude, aligned_time | ||
| Eta_e | magnitude, time | ||
| FluxPercentileRatioMid20 | magnitude | ||
| FluxPercentileRatioMid35 | magnitude | ||
| FluxPercentileRatioMid50 | magnitude | ||
| FluxPercentileRatioMid65 | magnitude | ||
| FluxPercentileRatioMid80 | magnitude | ||
| Freq{i}_harmonics_amplitude_{j} | Freq{i}_harmonics_amplitude_{j} and Freq{i}_harmonics_rel_phase_{j} | magnitude, time | |
| Gskew | magnitude | ||
| LinearTrend | magnitude, time | ||
| MaxSlope | magnitude, time | ||
| Mean | magnitude | ||
| Meanvariance | magnitude | ||
| MedianAbsDev | magnitude | ||
| MedianBRP | magnitude | ||
| PairSlopeTrend | magnitude | ||
| PercentAmplitude | magnitude | ||
| PercentDifferenceFluxPercentile | magnitude | ||
| PeriodLS | Period_fit, Psi_eta, Psi_CS | magnitude, time | |
| Period_fit | Psi_eta, PeriodLS, Psi_CS | magnitude, time | |
| Psi_CS | Period_fit, Psi_eta, PeriodLS | magnitude, time | |
| Psi_eta | Period_fit, PeriodLS, Psi_CS | magnitude, time | |
| Q31 | magnitude | ||
| Q31_color | aligned_magnitude2, aligned_magnitude | ||
| Rcs | magnitude | ||
| Skew | magnitude | ||
| SlottedA_length | magnitude, time | ||
| SmallKurtosis | magnitude | ||
| Std | magnitude | ||
| StetsonJ | aligned_magnitude2, aligned_magnitude, aligned_error, aligned_error2 | ||
| StetsonK | magnitude, error | ||
| StetsonK_AC | magnitude, error, time | ||
| StetsonL | aligned_magnitude2, aligned_magnitude, aligned_error, aligned_error2 | ||
| StructureFunction_index_21 | StructureFunction_index_32, StructureFunction_index_31 | magnitude, time | |
| StructureFunction_index_31 | StructureFunction_index_21, StructureFunction_index_32 | magnitude, time | |
| StructureFunction_index_32 | StructureFunction_index_21, StructureFunction_index_31 | magnitude, time |
The possible ways of how an user can choose the features from the library to be calculated are presented next.
List of features as an input:¶
The user can specify a list of features as input by specifying the
features as a list for the parameter only. In the following example,
we aim to calculate the standard deviation and Stetson L of the data:
In [10]:
fs = feets.FeatureSpace(only=['Std','StetsonL'])
features, values = fs.extract(*lc)
as_table(features, values)
Out[10]:
| Feature | Value |
|---|---|
| Std | 0.141573174959 |
| StetsonL | 0.58237036372 |
You can provide the same parameters one by one or by keyword intead of
use the unpacking *lc way. So the following examples will work:
lc(time, mag, error,
mag2, atime, amag, amag2,
aerror, aerror2)
or
lc(time=time, magnitude=mag, error=error,
magnitude2=mag2, aligned_time=atime,
aligned_magnitude=amag, aligned_magnitude2=amag2,
aligned_error=aerror, aligned_error2=aerror2)
Available data as an input:¶
In case the user does not have all the input vectors mentioned above, it
is necessary to specify the available data by specifying the list of
vectors using the parameter data. In the example below, we calculate
all the features that can be computed with the magnitude and time as an
input.
In [11]:
fs = feets.FeatureSpace(data=['magnitude','time'])
features, values = fs.extract(*lc)
as_table(features, values)
Out[11]:
| Feature | Value |
|---|---|
| Amplitude | 0.265 |
| AndersonDarling | 1.0 |
| Autocor_length | 1.0 |
| Con | 0.0 |
| Eta_e | 905.636200812 |
| FluxPercentileRatioMid20 | 0.0913140311804 |
| FluxPercentileRatioMid35 | 0.178173719376 |
| FluxPercentileRatioMid50 | 0.316258351893 |
| FluxPercentileRatioMid65 | 0.523385300668 |
| FluxPercentileRatioMid80 | 0.799554565702 |
| Freq1_harmonics_amplitude_0 | 0.132971918867 |
| Freq1_harmonics_amplitude_1 | 0.0770819007194 |
| Freq1_harmonics_amplitude_2 | 0.0497038938234 |
| Freq1_harmonics_amplitude_3 | 0.0253287258167 |
| Freq1_harmonics_rel_phase_0 | 0.0 |
| Freq1_harmonics_rel_phase_1 | 0.115067718485 |
| Freq1_harmonics_rel_phase_2 | 0.334299267194 |
| Freq1_harmonics_rel_phase_3 | 0.530855576474 |
| Freq2_harmonics_amplitude_0 | 0.0181114566827 |
| Freq2_harmonics_amplitude_1 | 0.0090622502799 |
| Freq2_harmonics_amplitude_2 | 0.00260631629629 |
| Freq2_harmonics_amplitude_3 | 0.00439984317964 |
| Freq2_harmonics_rel_phase_0 | 0.0 |
| Freq2_harmonics_rel_phase_1 | 0.641672610593 |
| Freq2_harmonics_rel_phase_2 | 1.68983485975 |
| Freq2_harmonics_rel_phase_3 | -1.20002370194 |
| Freq3_harmonics_amplitude_0 | 0.0167797089051 |
| Freq3_harmonics_amplitude_1 | 0.00322942122796 |
| Freq3_harmonics_amplitude_2 | 0.00366435564108 |
| Freq3_harmonics_amplitude_3 | 0.00435784547109 |
| Freq3_harmonics_rel_phase_0 | 0.0 |
| Freq3_harmonics_rel_phase_1 | 0.441761624287 |
| Freq3_harmonics_rel_phase_2 | -0.0264019762482 |
| Freq3_harmonics_rel_phase_3 | -0.361561445702 |
| Gskew | 0.2455 |
| LinearTrend | 6.17365857681e-06 |
| MaxSlope | 54.7252583612 |
| Mean | -5.91798911223 |
| Meanvariance | -0.0239225135894 |
| MedianAbsDev | 0.0545 |
| MedianBRP | 0.745393634841 |
| PairSlopeTrend | 0.0333333333333 |
| PercentAmplitude | -0.113085757398 |
| PercentDifferenceFluxPercentile | -0.0752787325006 |
| PeriodLS | 0.936942217405 |
| Period_fit | 0.0 |
| Psi_CS | 0.188077038434 |
| Psi_eta | 0.707845086624 |
| Q31 | 0.141 |
| Rcs | 0.0391714507727 |
| Skew | 0.956469867559 |
| SlottedA_length | 1.0 |
| SmallKurtosis | 1.37947868013 |
| Std | 0.141573174959 |
| StructureFunction_index_21 | 2.04757219899 |
| StructureFunction_index_31 | 3.12766185693 |
| StructureFunction_index_32 | 1.69906462906 |
List of features and available data as an input.¶
It is also possible to provide the available time series input vectors and calculate all possible features from a feature list using this data:
In [12]:
fs = feets.FeatureSpace(
only=['Mean','Beyond1Std','CAR_sigma','Color','SlottedA_length'],
data=['magnitude', 'error'])
features, values = fs.extract(*lc)
as_table(features, values)
Out[12]:
| Feature | Value |
|---|---|
| Beyond1Std | 0.222780569514 |
| Mean | -5.91798911223 |
Excluding list as an input¶
The user can also create a list of features to be excluded from the
calculation. To do so, the list of features to be excluded can be passed
as a list via the parameter exclude. For example:
In [13]:
fs = feets.FeatureSpace(
only=['Mean','Beyond1Std','CAR_sigma','Color','SlottedA_length'],
data=['magnitude', 'error'],
exclude=["Beyond1Std"])
features, values = fs.extract(*lc)
as_table(features, values)
Out[13]:
| Feature | Value |
|---|---|
| Mean | -5.91798911223 |
All the features¶
To calculate all the existing features in the library, the user only need to instantiate the feature space without parameters
In [14]:
fs = feets.FeatureSpace()
features, values = fs.extract(*lc)
as_table(features, values)
Out[14]:
| Feature | Value |
|---|---|
| Amplitude | 0.265 |
| AndersonDarling | 1.0 |
| Autocor_length | 1.0 |
| Beyond1Std | 0.222780569514 |
| CAR_mean | -9.2306988739 |
| CAR_sigma | -0.219280492988 |
| CAR_tau | 0.641120373773 |
| Color | -0.333255024533 |
| Con | 0.0 |
| Eta_color | 12930.6852576 |
| Eta_e | 905.636200812 |
| FluxPercentileRatioMid20 | 0.0913140311804 |
| FluxPercentileRatioMid35 | 0.178173719376 |
| FluxPercentileRatioMid50 | 0.316258351893 |
| FluxPercentileRatioMid65 | 0.523385300668 |
| FluxPercentileRatioMid80 | 0.799554565702 |
| Freq1_harmonics_amplitude_0 | 0.132971918867 |
| Freq1_harmonics_amplitude_1 | 0.0770819007194 |
| Freq1_harmonics_amplitude_2 | 0.0497038938234 |
| Freq1_harmonics_amplitude_3 | 0.0253287258167 |
| Freq1_harmonics_rel_phase_0 | 0.0 |
| Freq1_harmonics_rel_phase_1 | 0.115067718485 |
| Freq1_harmonics_rel_phase_2 | 0.334299267194 |
| Freq1_harmonics_rel_phase_3 | 0.530855576474 |
| Freq2_harmonics_amplitude_0 | 0.0181114566827 |
| Freq2_harmonics_amplitude_1 | 0.0090622502799 |
| Freq2_harmonics_amplitude_2 | 0.00260631629629 |
| Freq2_harmonics_amplitude_3 | 0.00439984317964 |
| Freq2_harmonics_rel_phase_0 | 0.0 |
| Freq2_harmonics_rel_phase_1 | 0.641672610593 |
| Freq2_harmonics_rel_phase_2 | 1.68983485975 |
| Freq2_harmonics_rel_phase_3 | -1.20002370194 |
| Freq3_harmonics_amplitude_0 | 0.0167797089051 |
| Freq3_harmonics_amplitude_1 | 0.00322942122796 |
| Freq3_harmonics_amplitude_2 | 0.00366435564108 |
| Freq3_harmonics_amplitude_3 | 0.00435784547109 |
| Freq3_harmonics_rel_phase_0 | 0.0 |
| Freq3_harmonics_rel_phase_1 | 0.441761624287 |
| Freq3_harmonics_rel_phase_2 | -0.0264019762482 |
| Freq3_harmonics_rel_phase_3 | -0.361561445702 |
| Gskew | 0.2455 |
| LinearTrend | 6.17365857681e-06 |
| MaxSlope | 54.7252583612 |
| Mean | -5.91798911223 |
| Meanvariance | -0.0239225135894 |
| MedianAbsDev | 0.0545 |
| MedianBRP | 0.745393634841 |
| PairSlopeTrend | 0.0333333333333 |
| PercentAmplitude | -0.113085757398 |
| PercentDifferenceFluxPercentile | -0.0752787325006 |
| PeriodLS | 0.936942217405 |
| Period_fit | 0.0 |
| Psi_CS | 0.188077038434 |
| Psi_eta | 0.707845086624 |
| Q31 | 0.141 |
| Q31_color | 0.106 |
| Rcs | 0.0391714507727 |
| Skew | 0.956469867559 |
| SlottedA_length | 1.0 |
| SmallKurtosis | 1.37947868013 |
| Std | 0.141573174959 |
| StetsonJ | 1.39841114014 |
| StetsonK | 0.690626626289 |
| StetsonK_AC | 0.812563161458 |
| StetsonL | 0.58237036372 |
| StructureFunction_index_21 | 2.04757219899 |
| StructureFunction_index_31 | 3.12766185693 |
| StructureFunction_index_32 | 1.69906462906 |
Required data
The FeatureSpace object auto generates the set of required data
(stored in FeatureSpace.required_data_) based on the data,
only and exclude params. If you not provide the required data
when you excecute the extract() method, an exception is raised. For
example
In [15]:
fs = feets.FeatureSpace(only=["PeriodLS"])
fs.required_data_
Out[15]:
frozenset({u'magnitude', u'time'})
In [16]:
%%expect_exception feets.DataRequiredError
fs.extract(time=time)
--------------------------------------------------------------
DataRequiredError Traceback (most recent call last)
<ipython-input-16-4a8c13f433b2> in <module>()
1
----> 2 fs.extract(time=time)
/home/jbcabral/projects/feets/src/feets/core.pyc in extract(self, time, magnitude, error, magnitude2, aligned_time, aligned_magnitude, aligned_magnitude2, aligned_error, aligned_error2)
286 DATA_ALIGNED_MAGNITUDE2: aligned_magnitude2,
287 DATA_ALIGNED_ERROR: aligned_error,
--> 288 DATA_ALIGNED_ERROR2: aligned_error2})
289
290 features = {}
/home/jbcabral/projects/feets/src/feets/core.pyc in dict_data_as_array(self, d)
268 for k, v in d.items():
269 if k in self._required_data and v is None:
--> 270 raise DataRequiredError(k)
271 array_data[k] = v if v is None else np.asarray(v)
272 return array_data
DataRequiredError: magnitude
Features Calculation Precedence¶
As showed the parameters data, only and exclude can be
combinded and the selected features will be calculated in three steps:
- The
FeatureSpaceselect all the features available for the availabledata, otherwise all the features are selected. - If the
onlyparameter is notNonethen the selected features from the step 1 are filtered only if they exist in theonlylist. - If
excludeis notNone, then removes the features selected by the step 1 and 2 that are also inexlude
Library output¶
When calculating the features of a light-curve, the output are two different array.
- The first one are the names of the calculated features, where thr \(i_{nth}\) element represent the name of the \(i_{nth}\) feature.
- The second array are the values of the features in the same order that the names.
So for example if we want to print the name and the value of the 3rd feature:
In [17]:
fs = feets.FeatureSpace()
features, values = fs.extract(*lc)
print(features[2], "=", values[2])
Autocor_length = 1.0
Inother hand this format can be easily converted into a dictionary with the next code:
In [18]:
fdict = dict(zip(features, values))
fdict
Out[18]:
{u'Amplitude': 0.26500000000000057,
u'AndersonDarling': 1.0,
u'Autocor_length': 1.0,
u'Beyond1Std': 0.22278056951423786,
u'CAR_mean': -9.230698873903961,
u'CAR_sigma': -0.21928049298842511,
u'CAR_tau': 0.64112037377348619,
u'Color': -0.33325502453332145,
u'Con': 0.0,
u'Eta_color': 12930.685257570141,
u'Eta_e': 905.63620081228805,
u'FluxPercentileRatioMid20': 0.091314031180401739,
u'FluxPercentileRatioMid35': 0.1781737193763922,
u'FluxPercentileRatioMid50': 0.3162583518930947,
u'FluxPercentileRatioMid65': 0.52338530066815037,
u'FluxPercentileRatioMid80': 0.79955456570155925,
u'Freq1_harmonics_amplitude_0': 0.13297191886665682,
u'Freq1_harmonics_amplitude_1': 0.077081900719377316,
u'Freq1_harmonics_amplitude_2': 0.049703893823420386,
u'Freq1_harmonics_amplitude_3': 0.025328725816726485,
u'Freq1_harmonics_rel_phase_0': 0.0,
u'Freq1_harmonics_rel_phase_1': 0.11506771848541875,
u'Freq1_harmonics_rel_phase_2': 0.33429926719365932,
u'Freq1_harmonics_rel_phase_3': 0.53085557647407389,
u'Freq2_harmonics_amplitude_0': 0.018111456682708856,
u'Freq2_harmonics_amplitude_1': 0.009062250279899587,
u'Freq2_harmonics_amplitude_2': 0.002606316296287086,
u'Freq2_harmonics_amplitude_3': 0.0043998431796405972,
u'Freq2_harmonics_rel_phase_0': 0.0,
u'Freq2_harmonics_rel_phase_1': 0.64167261059311065,
u'Freq2_harmonics_rel_phase_2': 1.6898348597478692,
u'Freq2_harmonics_rel_phase_3': -1.2000237019387199,
u'Freq3_harmonics_amplitude_0': 0.016779708905107649,
u'Freq3_harmonics_amplitude_1': 0.0032294212279590758,
u'Freq3_harmonics_amplitude_2': 0.0036643556410844678,
u'Freq3_harmonics_amplitude_3': 0.0043578454710941801,
u'Freq3_harmonics_rel_phase_0': 0.0,
u'Freq3_harmonics_rel_phase_1': 0.44176162428687271,
u'Freq3_harmonics_rel_phase_2': -0.026401976248181636,
u'Freq3_harmonics_rel_phase_3': -0.36156144570222293,
u'Gskew': 0.24549999999999983,
u'LinearTrend': 6.1736585768121618e-06,
u'MaxSlope': 54.725258361167832,
u'Mean': -5.9179891122278052,
u'Meanvariance': -0.023922513589418142,
u'MedianAbsDev': 0.054499999999999993,
u'MedianBRP': 0.74539363484087107,
u'PairSlopeTrend': 0.033333333333333333,
u'PercentAmplitude': -0.11308575739793782,
u'PercentDifferenceFluxPercentile': -0.075278732500628692,
u'PeriodLS': 0.93694221740476769,
u'Period_fit': 0.0,
u'Psi_CS': 0.18807703843435905,
u'Psi_eta': 0.70784508662419521,
u'Q31': 0.14100000000000001,
u'Q31_color': 0.10600000000000076,
u'Rcs': 0.039171450772665782,
u'Skew': 0.95646986755937902,
u'SlottedA_length': 1.0,
u'SmallKurtosis': 1.3794786801255068,
u'Std': 0.14157317495929828,
u'StetsonJ': 1.3984111401436403,
u'StetsonK': 0.69062662628891813,
u'StetsonK_AC': 0.81256316145779794,
u'StetsonL': 0.5823703637198997,
u'StructureFunction_index_21': 2.0475721989892599,
u'StructureFunction_index_31': 3.1276618569316184,
u'StructureFunction_index_32': 1.6990646290639937}
Ploting the example lightcurve in phase¶
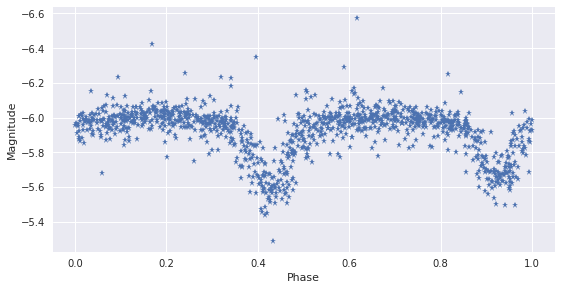
Note: for periodic light-curves we are able to transform the photometric time series into a single light-curve in which each period is mapped onto the same time axis as follows:
where \(T\) is the period, \(t_0\) is an arbitrary starting point and the symbol \(\{\}\) represents the non-integer part of the fraction. This process produces a folded light-curve on an x-axis of folded time that ranges from 0 to 1. The corresponding folded light-curve of the previous example is shown next:
In [19]:
T = 2 * fdict["PeriodLS"]
new_b = np.mod(lc[0], T) / T;
idx = np.argsort(2 * new_b)
plt.plot(new_b, lc[1], '*')
plt.xlabel("Phase")
plt.ylabel("Magnitude")
plt.gca().invert_yaxis()
The Features¶
The next section details the features that we have developed in order to represent light curves. For each feature, we also describe a benchmark test performed in order to test the feature’s correctness.
Each feature was also tested to ensure invariability to unequal sampling. Because telescope observations are not always taken at uniformly spaced intervals, the light curve features should be invariant to this non-uniformity. These test can be found here
Let’s first assume the existence of some synthetic light-curves in order to explain each one of the features extractors along the library:
lc_normal: its magnitude follows a Gaussian distributionlc_periodic: its magnitude has a periodic variabilitylc_uniform: its magnitude follows a uniform distribution
In [20]:
features_doc()
Out[20]:
Amplitude Extactor
Amplitude
The amplitude is defined as the half of the difference between the median of the maximum 5% and the median of the minimum 5% magnitudes. For a sequence of numbers from 0 to 1000 the amplitude should be equal to 475.5.
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
AndersonDarling Extactor
AndersonDarling
The Anderson-Darling test is a statistical test of whether a given sample of data is drawn from a given probability distribution. When applied to testing if a normal distribution adequately describes a set of data, it is one of the most powerful statistical tools for detecting most departures from normality.
For a normal distribution the Anderson-Darling statistic should take values close to 0.25.
References
kim2009trending Kim, D. W., Protopapas, P., Alcock, C., Byun, Y. I., & Bianco, F. (2009). De-Trending Time Series for Astronomical Variability Surveys. Monthly Notices of the Royal Astronomical Society, 397(1), 558-568. Doi:10.1111/j.1365-2966.2009.14967.x.
Required Data
Full list of features
Parameters
Dependencies
AutocorLength Extactor
Autocor_length
The autocorrelation, also known as serial correlation, is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time lag between them. It is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies.
For an observed series \(y_1, y_2,\dots,y_T\) with sample mean \(\bar{y}\) , the sample lag \(-h\) autocorrelation is given by:
\(\rho_h = \frac{\sum_{t=h+1}^T (y_t - \bar{y})(y_{t-h}-\bar{y})} {\sum_{t=1}^T (y_t - \bar{y})^2}\)Since the autocorrelation fuction of a light curve is given by a vector and we can only return one value as a feature, we define the length of the autocorrelation function where its value is smaller than \(e^{-1}\) .
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
Required Data
Full list of features
Parameters
100
Dependencies
Beyond1Std Extactor
Beyond1Std
Percentage of points beyond one standard deviation from the weighted mean. For a normal distribution, it should take a value close to 0.32:
>>> fs = feets.FeatureSpace(only=['Beyond1Std']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Beyond1Std': 0.317}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
CAR Extactor
- In order to model the irregular sampled times series we use CAR
-
(Brockwell and Davis, 2002), a continious time auto regressive model.
CAR process has three parameters, it provides a natural and consistent way of estimating a characteristic time scale and variance of light-curves. CAR process is described by the following stochastic differential equation:
\begin{align*} dX(t) = - \frac{1}{\tau} X(t)dt + \sigma_C \sqrt{dt} \epsilon(t) + bdt, \\ for \: \tau, \sigma_C, t \geq 0 \end{align*}where the mean value of the lightcurve \(X(t)\) is \(b\tau\) and the variance is \(\frac{\tau\sigma_C^2}{2}\) . \(\tau\) is the relaxation time of the process \(X(t)\) , it can be interpreted as describing the variability amplitude of the time series. \(\sigma_C\) can be interpreted as describing the variability of the time series on time scales shorter than \(\tau\) . \(\epsilon(t)\) is a white noise process with zero mean and variance equal to one.
The likelihood function of a CAR model for a light-curve with observations \(x - \{x_1, \dots, x_n\}\) observed at times \(\{t_1, \dots, t_n\}\) with measurements error variances \(\{\delta_1^2, \dots, \delta_n^2\}\) is:
\begin{align*} p (x|b,\sigma_C,\tau) = \prod_{i=1}^n \frac{1}{ [2 \pi (\Omega_i + \delta_i^2 )]^{1/2}} exp \{-\frac{1}{2} \frac{(\hat{x}_i - x^*_i )^2}{\Omega_i + \delta^2_i}\} \\ \end{align*}\begin{align*} x_i^* = x_i - b\tau \\ \end{align*}\begin{align*} \hat{x}_0 = 0 \\ \end{align*}\begin{align*} \Omega_0 = \frac{\tau \sigma^2_C}{2} \\ \end{align*}\begin{align*} \hat{x}_i = a_i\hat{x}_{i-1} + \frac{a_i \Omega_{i-1}}{\Omega_{i-1} + \delta^2_{i-1}} (x^*_{i-1} + \hat{x}_{i-1}) \\ \end{align*}\(\Omega_i = \Omega_0 (1- a_i^2 ) + a_i^2 \Omega_{i-1} (1 - \frac{\Omega_{i-1}}{\Omega_{i-1} + \delta^2_{i-1}} )\)To find the optimal parameters we maximize the likelihood with respect to \(\sigma_C\) and \(\tau\) and calculate \(b\) as the mean magnitude of the light-curve divided by \(\tau\) .
>>> fs = feets.FeatureSpace( ... only=['CAR_sigma', 'CAR_tau','CAR_mean']) >>> features, values = fs.extract(**lc_periodic) >>> dict(zip(features, values)) {'CAR_mean': -9.230698873903961, 'CAR_sigma': -0.21928049298842511, 'CAR_tau': 0.64112037377348619}
References
pichara2012improved Pichara, K., Protopapas, P., Kim, D. W., Marquette, J. B., & Tisserand, P. (2012). An improved quasar detection method in EROS-2 and MACHO LMC data sets. Monthly Notices of the Royal Astronomical Society, 427(2), 1284-1297. Doi:10.1111/j.1365-2966.2012.22061.x.
Required Data
Full list of features
Parameters
nelder-mead
Dependencies
Color Extactor
Color
The color is defined as the difference between the average magnitude of two different bands observations.
>>> fs = feets.FeatureSpace(only=['Color']) >>> features, values = fs.extract(**lc) >>> dict(zip(features, values)) {'Color': -0.33325502453332145}
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
Required Data
Full list of features
Parameters
Dependencies
Con Extactor
Con
Index introduced for the selection of variable stars from the OGLE database (Wozniak 2000). To calculate Con, we count the number of three consecutive data points that are brighter or fainter than \(2\sigma\) and normalize the number by \(N−2\) .
For a normal distribution and by considering just one star, Con should take values close to 0.045:
>>> fs = feets.FeatureSpace(only=['Con']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Con': 0.0476}
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
Required Data
Full list of features
Parameters
3
Dependencies
EtaColor Extactor
Eta_color ( \(\eta_{color}\) )
Variability index Eta_e ( \(\eta^e\) ) calculated from the color light-curve.
>>> fs = feets.FeatureSpace(only=['Eta_color']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Eta_color': 1.991749074648397}
References
kim2014epoch Kim, D. W., Protopapas, P., Bailer-Jones, C. A., Byun, Y. I., Chang, S. W., Marquette, J. B., & Shin, M. S. (2014). The EPOCH Project: I. Periodic Variable Stars in the EROS-2 LMC Database. arXiv preprint Doi:10.1051/0004-6361/201323252.
Required Data
Full list of features
Parameters
Dependencies
Eta_e Extactor
Eta_e ( \(\eta^e\) )
Variability index \(\eta\) is the ratio of the mean of the square of successive differences to the variance of data points. The index was originally proposed to check whether the successive data points are independent or not. In other words, the index was developed to check if any trends exist in the data (von Neumann 1941). It is defined as:
\(\eta = \frac{1}{(N-1)\sigma^2} \sum_{i=1}^{N-1} (m_{i+1}-m_i)^2\)The variability index should take a value close to 2 for a normal distribution.
Although \(\eta\) is a powerful index for quantifying variability characteristics of a time series, it does not take into account unequal sampling. Thus \(\eta^r\) is defined as:
\(\eta^e = \bar{w} \, (t_{N-1} - t_1)^2 \frac{\sum_{i=1}^{N-1} w_i (m_{i+1} - m_i)^2} {\sigma^2 \sum_{i=1}^{N-1} w_i}\)Where:
\(w_i = \frac{1}{(t_{i+1} - t_i)^2}\)Example:
>>> fs = feets.FeatureSpace(only=['Eta_e']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Eta_e': 2.0028592616231866}
References
kim2014epoch Kim, D. W., Protopapas, P., Bailer-Jones, C. A., Byun, Y. I., Chang, S. W., Marquette, J. B., & Shin, M. S. (2014). The EPOCH Project: I. Periodic Variable Stars in the EROS-2 LMC Database. arXiv preprint Doi:10.1051/0004-6361/201323252.
Required Data
Full list of features
Parameters
Dependencies
FluxPercentileRatioMid20 Extactor
In order to caracterize the sorted magnitudes distribution we use percentiles. If \(F_{5, 95}\) is the difference between 95% and 5% magnitude values, we calculate the following:
- flux_percentile_ratio_mid20: ratio \(F_{40, 60}/F_{5, 95}\)
- flux_percentile_ratio_mid35: ratio \(F_{32.5, 67.5}/F_{5, 95}\)
- flux_percentile_ratio_mid50: ratio \(F_{25, 75}/F_{5, 95}\)
- flux_percentile_ratio_mid65: ratio \(F_{17.5, 82.5}/F_{5, 95}\)
- flux_percentile_ratio_mid80: ratio \(F_{10, 90}/F_{5, 95}\)
For the first feature for example, in the case of a normal distribution, this is equivalente to calculate:
\(\frac{erf^{-1}(2 \cdot 0.6-1)-erf^{-1}(2 \cdot 0.4-1)} {erf^{-1}(2 \cdot 0.95-1)-erf^{-1}(2 \cdot 0.05-1)}\)So, the expected values for each of the flux percentile features are:
- flux_percentile_ratio_mid20 = 0.154
- flux_percentile_ratio_mid35 = 0.275
- flux_percentile_ratio_mid50 = 0.410
- flux_percentile_ratio_mid65 = 0.568
- flux_percentile_ratio_mid80 = 0.779
References
| richards2011machine | Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10. |
|---|
Required Data
Full list of features
Parameters
Dependencies
FluxPercentileRatioMid35 Extactor
In order to caracterize the sorted magnitudes distribution we use percentiles. If \(F_{5, 95}\) is the difference between 95% and 5% magnitude values, we calculate the following:
- flux_percentile_ratio_mid20: ratio \(F_{40, 60}/F_{5, 95}\)
- flux_percentile_ratio_mid35: ratio \(F_{32.5, 67.5}/F_{5, 95}\)
- flux_percentile_ratio_mid50: ratio \(F_{25, 75}/F_{5, 95}\)
- flux_percentile_ratio_mid65: ratio \(F_{17.5, 82.5}/F_{5, 95}\)
- flux_percentile_ratio_mid80: ratio \(F_{10, 90}/F_{5, 95}\)
For the first feature for example, in the case of a normal distribution, this is equivalente to calculate:
\(\frac{erf^{-1}(2 \cdot 0.6-1)-erf^{-1}(2 \cdot 0.4-1)} {erf^{-1}(2 \cdot 0.95-1)-erf^{-1}(2 \cdot 0.05-1)}\)So, the expected values for each of the flux percentile features are:
- flux_percentile_ratio_mid20 = 0.154
- flux_percentile_ratio_mid35 = 0.275
- flux_percentile_ratio_mid50 = 0.410
- flux_percentile_ratio_mid65 = 0.568
- flux_percentile_ratio_mid80 = 0.779
References
| richards2011machine | Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10. |
|---|
Required Data
Full list of features
Parameters
Dependencies
FluxPercentileRatioMid50 Extactor
In order to caracterize the sorted magnitudes distribution we use percentiles. If \(F_{5, 95}\) is the difference between 95% and 5% magnitude values, we calculate the following:
- flux_percentile_ratio_mid20: ratio \(F_{40, 60}/F_{5, 95}\)
- flux_percentile_ratio_mid35: ratio \(F_{32.5, 67.5}/F_{5, 95}\)
- flux_percentile_ratio_mid50: ratio \(F_{25, 75}/F_{5, 95}\)
- flux_percentile_ratio_mid65: ratio \(F_{17.5, 82.5}/F_{5, 95}\)
- flux_percentile_ratio_mid80: ratio \(F_{10, 90}/F_{5, 95}\)
For the first feature for example, in the case of a normal distribution, this is equivalente to calculate:
\(\frac{erf^{-1}(2 \cdot 0.6-1)-erf^{-1}(2 \cdot 0.4-1)} {erf^{-1}(2 \cdot 0.95-1)-erf^{-1}(2 \cdot 0.05-1)}\)So, the expected values for each of the flux percentile features are:
- flux_percentile_ratio_mid20 = 0.154
- flux_percentile_ratio_mid35 = 0.275
- flux_percentile_ratio_mid50 = 0.410
- flux_percentile_ratio_mid65 = 0.568
- flux_percentile_ratio_mid80 = 0.779
References
| richards2011machine | Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10. |
|---|
Required Data
Full list of features
Parameters
Dependencies
FluxPercentileRatioMid65 Extactor
In order to caracterize the sorted magnitudes distribution we use percentiles. If \(F_{5, 95}\) is the difference between 95% and 5% magnitude values, we calculate the following:
- flux_percentile_ratio_mid20: ratio \(F_{40, 60}/F_{5, 95}\)
- flux_percentile_ratio_mid35: ratio \(F_{32.5, 67.5}/F_{5, 95}\)
- flux_percentile_ratio_mid50: ratio \(F_{25, 75}/F_{5, 95}\)
- flux_percentile_ratio_mid65: ratio \(F_{17.5, 82.5}/F_{5, 95}\)
- flux_percentile_ratio_mid80: ratio \(F_{10, 90}/F_{5, 95}\)
For the first feature for example, in the case of a normal distribution, this is equivalente to calculate:
\(\frac{erf^{-1}(2 \cdot 0.6-1)-erf^{-1}(2 \cdot 0.4-1)} {erf^{-1}(2 \cdot 0.95-1)-erf^{-1}(2 \cdot 0.05-1)}\)So, the expected values for each of the flux percentile features are:
- flux_percentile_ratio_mid20 = 0.154
- flux_percentile_ratio_mid35 = 0.275
- flux_percentile_ratio_mid50 = 0.410
- flux_percentile_ratio_mid65 = 0.568
- flux_percentile_ratio_mid80 = 0.779
References
| richards2011machine | Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10. |
|---|
Required Data
Full list of features
Parameters
Dependencies
FluxPercentileRatioMid80 Extactor
In order to caracterize the sorted magnitudes distribution we use percentiles. If \(F_{5, 95}\) is the difference between 95% and 5% magnitude values, we calculate the following:
- flux_percentile_ratio_mid20: ratio \(F_{40, 60}/F_{5, 95}\)
- flux_percentile_ratio_mid35: ratio \(F_{32.5, 67.5}/F_{5, 95}\)
- flux_percentile_ratio_mid50: ratio \(F_{25, 75}/F_{5, 95}\)
- flux_percentile_ratio_mid65: ratio \(F_{17.5, 82.5}/F_{5, 95}\)
- flux_percentile_ratio_mid80: ratio \(F_{10, 90}/F_{5, 95}\)
For the first feature for example, in the case of a normal distribution, this is equivalente to calculate:
\(\frac{erf^{-1}(2 \cdot 0.6-1)-erf^{-1}(2 \cdot 0.4-1)} {erf^{-1}(2 \cdot 0.95-1)-erf^{-1}(2 \cdot 0.05-1)}\)So, the expected values for each of the flux percentile features are:
- flux_percentile_ratio_mid20 = 0.154
- flux_percentile_ratio_mid35 = 0.275
- flux_percentile_ratio_mid50 = 0.410
- flux_percentile_ratio_mid65 = 0.568
- flux_percentile_ratio_mid80 = 0.779
References
| richards2011machine | Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10. |
|---|
Required Data
Full list of features
Parameters
Dependencies
FourierComponents Extactor
Periodic features extracted from light-curves using Lomb–Scargle (Richards et al., 2011)
Here, we adopt a model where the time series of the photometric magnitudes of variable stars is modeled as a superposition of sines and cosines:
\(y_i(t|f_i) = a_i\sin(2\pi f_i t) + b_i\cos(2\pi f_i t) + b_{i,\circ}\)where \(a\) and \(b\) are normalization constants for the sinusoids of frequency \(f_i\) and \(b_{i,\circ}\) is the magnitude offset.
To find periodic variations in the data, we fit the equation above by minimizing the sum of squares, which we denote \(\chi^2\) :
\(\chi^2 = \sum_k \frac{(d_k - y_i(t_k))^2}{\sigma_k^2}\)where \(\sigma_k\) is the measurement uncertainty in data point \(d_k\) . We allow the mean to float, leading to more robust period estimates in the case where the periodic phase is not uniformly sampled; in these cases, the model light curve has a non-zero mean. This can be important when searching for periods on the order of the data span \(T_{tot}\) . Now, define
\(\chi^2_{\circ} = \sum_k \frac{(d_k - \mu)^2}{\sigma_k^2}\)where \(\mu\) is the weighted mean
\(\mu = \frac{\sum_k d_k / \sigma_k^2}{\sum_k 1/\sigma_k^2}\)Then, the generalized Lomb-Scargle periodogram is:
\(P_f(f) = \frac{(N-1)}{2} \frac{\chi_{\circ}^2 - \chi_m^2(f)} {\chi_{\circ}^2}\)where \(\chi_m^2(f)\) is \(\chi^2\) minimized with respect to \(a, b\) and \(b_{\circ}\) .
Following Debosscher et al. (2007), we fit each light curve with a linear term plus a harmonic sum of sinusoids:
\(y(t) = ct + \sum_{i=1}^{3}\sum_{j=1}^{4} y_i(t|jf_i)\)where each of the three test frequencies \(f_i\) is allowed to have four harmonics at frequencies \(f_{i,j} = jf_i\) . The three test frequencies \(f_i\) are found iteratively, by successfully finding and removing periodic signal producing a peak in \(P_f(f)\) , where \(P_f(f)\) is the Lomb-Scargle periodogram as defined above.
Given a peak in \(P_f(f)\) , we whiten the data with respect to that frequency by fitting away a model containing that frequency as well as components with frequencies at 2, 3, and 4 times that fundamental frequency (harmonics). Then, we subtract that model from the data, update \(\chi_{\circ}^2\) , and recalculate \(P_f(f)\) to find more periodic components.
Algorithm:
- For \(i = {1, 2, 3}\)
- Calculate Lomb-Scargle periodogram \(P_f(f)\) for light curve.
- Find peak in \(P_f(f)\) , subtract that model from data.
- Update \(\chi_{\circ}^2\) , return to Step 1.
Then, the features extracted are given as an amplitude and a phase:
\begin{align*} A_{i,j} = \sqrt{a_{i,j}^2 + b_{i,j}^2}\\ \textrm{PH}_{i,j} = \arctan(\frac{b_{i,j}}{a_{i,j}}) \end{align*}where \(A_{i,j}\) is the amplitude of the \(j-th\) harmonic of the \(i-th\) frequency component and \(\textrm{PH}_{i,j}\) is the phase component, which we then correct to a relative phase with respect to the phase of the first component:
\(\textrm{PH}'_{i,j} = \textrm{PH}_{i,j} - \textrm{PH}_{00}\)and remapped to \(|-\pi, +\pi|\)
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
{u'autopower_kwds': {u'nyquist_factor': 100, u'normalization': u'standard'}}
Dependencies
Gskew Extactor
Median-of-magnitudes based measure of the skew.
\(Gskew = m_{q3} + m_{q97} - 2m\)Where:
- \(m_{q3}\) is the median of magnitudes lesser or equal than the quantile 3.
- \(m_{q97}\) is the median of magnitudes greater or equal than the quantile 97.
- \(m\) is the median of magnitudes.
Required Data
Full list of features
Parameters
Dependencies
LinearTrend Extactor
LinearTrend
Slope of a linear fit to the light-curve.
>>> fs = feets.FeatureSpace(only=['LinearTrend']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'LinearTrend': -3.2084065290292509e-06}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
LombScargle Extactor
PeriodLS
The Lomb-Scargle (L-S) algorithm (Scargle, 1982) is a variation of the Discrete Fourier Transform (DFT), in which a time series is decomposed into a linear combination of sinusoidal functions. The basis of sinusoidal functions transforms the data from the time domain to the frequency domain. DFT techniques often assume evenly spaced data points in the time series, but this is rarely the case with astrophysical time-series data. Scargle has derived a formula for transform coefficients that is similiar to the DFT in the limit of evenly spaced observations. In addition, an adjustment of the values used to calculate the transform coefficients makes the transform invariant to time shifts.
The Lomb-Scargle periodogram is optimized to identify sinusoidal-shaped periodic signals in time-series data. Particular applications include radial velocity data and searches for pulsating variable stars. L-S is not optimal for detecting signals from transiting exoplanets, where the shape of the periodic light-curve is not sinusoidal.
Next, we perform a test on the synthetic periodic light-curve we created (which period is 20) to confirm the accuracy of the period found by the L-S method
Period_fit
The false alarm probability of the largest periodogram value. Let's test it for a normal distributed data and for a periodic one.
Psi_CS ( \(\Psi_{CS}\) )
\(R_{CS}\) applied to the phase-folded light curve (generated using the period estimated from the Lomb-Scargle method).
Psi_eta ( \(\Psi_{\eta}\) )
\(\eta^e\) index calculated from the folded light curve.
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
kim2014epoch Kim, D. W., Protopapas, P., Bailer-Jones, C. A., Byun, Y. I., Chang, S. W., Marquette, J. B., & Shin, M. S. (2014). The EPOCH Project: I. Periodic Variable Stars in the EROS-2 LMC Database. arXiv preprint Doi:10.1051/0004-6361/201323252.
Required Data
Full list of features
Parameters
{u'autopower_kwds': {u'nyquist_factor': 100, u'normalization': u'standard'}}
{u'method': u'simple', u'normalization': u'standard'}
Dependencies
MaxSlope Extactor
MaxSlope
Maximum absolute magnitude slope between two consecutive observations.
Examining successive (time-sorted) magnitudes, the maximal first difference (value of delta magnitude over delta time)
>>> fs = feets.FeatureSpace(only=['MaxSlope']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'MaxSlope': 5.4943105823904741}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
True
Dependencies
Mean Extactor
Mean
Mean magnitude. For a normal distribution it should take a value close to zero:
>>> fs = feets.FeatureSpace(only=['Mean']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Mean': 0.0082611563419413246}
References
kim2014epoch Kim, D. W., Protopapas, P., Bailer-Jones, C. A., Byun, Y. I., Chang, S. W., Marquette, J. B., & Shin, M. S. (2014). The EPOCH Project: I. Periodic Variable Stars in the EROS-2 LMC Database. arXiv preprint Doi:10.1051/0004-6361/201323252.
Required Data
Full list of features
Parameters
Dependencies
MeanVariance Extactor
Meanvariance ( \(\frac{\sigma}{\bar{m}}\) )
This is a simple variability index and is defined as the ratio of the standard deviation \(\sigma\) , to the mean magnitude, \(\bar{m}\) . If a light curve has strong variability, \(\frac{\sigma}{\bar{m}}\) of the light curve is generally large.
For a uniform distribution from 0 to 1, the mean is equal to 0.5 and the variance is equal to 1/12, thus the mean-variance should take a value close to 0.577:
>>> fs = feets.FeatureSpace(only=['Meanvariance']) >>> features, values = fs.extract(**lc_uniform) >>> dict(zip(features, values)) {'Meanvariance': 0.5816791217381897}
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
Required Data
Full list of features
Parameters
Dependencies
MedianAbsDev Extactor
MedianAbsDev
The median absolute deviation is defined as the median discrepancy of the data from the median data:
\(Median Absolute Deviation = median(|mag - median(mag)|)\)It should take a value close to 0.675 for a normal distribution:
>>> fs = feets.FeatureSpace(only=['MedianAbsDev']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'MedianAbsDev': 0.66332131466690614}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
MedianBRP Extactor
MedianBRP (Median buffer range percentage)
Fraction (<= 1) of photometric points within amplitude/10 of the median magnitude
>>> fs = feets.FeatureSpace(only=['MedianBRP']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'MedianBRP': 0.559}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
PairSlopeTrend Extactor
PairSlopeTrend
Considering the last 30 (time-sorted) measurements of source magnitude, the fraction of increasing first differences minus the fraction of decreasing first differences.
>>> fs = feets.FeatureSpace(only=['PairSlopeTrend']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'PairSlopeTrend': -0.16666666666666666}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
PercentAmplitude Extactor
PercentAmplitude
Largest percentage difference between either the max or min magnitude and the median.
>>> fs = feets.FeatureSpace(only=['PercentAmplitude']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'PercentAmplitude': -168.991253993057}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
PercentDifferenceFluxPercentile Extactor
PercentDifferenceFluxPercentile
Ratio of \(F_{5, 95}\) over the median magnitude.
>>> fs = feets.FeatureSpace(only=['PercentDifferenceFluxPercentile']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'PercentDifferenceFluxPercentile': -134.93590403825007}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
Q31 Extactor
Q31 ( \(Q_{3-1}\) )
\(Q_{3-1}\) is the difference between the third quartile, \(Q_3\) , and the first quartile, \(Q_1\) , of a raw light curve. \(Q_1\) is a split between the lowest 25% and the highest 75% of data. \(Q_3\) is a split between the lowest 75% and the highest 25% of data.
>>> fs = feets.FeatureSpace(only=['Q31']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Q31': 1.3320376563134508}
References
kim2014epoch Kim, D. W., Protopapas, P., Bailer-Jones, C. A., Byun, Y. I., Chang, S. W., Marquette, J. B., & Shin, M. S. (2014). The EPOCH Project: I. Periodic Variable Stars in the EROS-2 LMC Database. arXiv preprint Doi:10.1051/0004-6361/201323252.
Required Data
Full list of features
Parameters
Dependencies
Q31Color Extactor
Q31_color ( \(Q_{3-1|B-R}\) )
\(Q_{3-1}\) applied to the difference between both bands of a light curve (B-R).
>>> fs = feets.FeatureSpace(only=['Q31_color']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Q31_color': 1.8840489594535512}
References
kim2014epoch Kim, D. W., Protopapas, P., Bailer-Jones, C. A., Byun, Y. I., Chang, S. W., Marquette, J. B., & Shin, M. S. (2014). The EPOCH Project: I. Periodic Variable Stars in the EROS-2 LMC Database. arXiv preprint Doi:10.1051/0004-6361/201323252.
Required Data
Full list of features
Parameters
Dependencies
RCS Extactor
Rcs - Range of cumulative sum ( \(R_{cs}\) )
\(R_{cs}\) is the range of a cumulative sum (Ellaway 1978) of each light-curve and is defined as:
\begin{align*} R_{cs} = max(S) - min(S) \\ S = \frac{1}{N \sigma} \sum_{i=1}^l (m_i - \bar{m}) \end{align*}where max(min) is the maximum (minimum) value of S and \(l=1,2, \dots, N\) .
\(R_{cs}\) should take a value close to zero for any symmetric distribution:
>>> fs = feets.FeatureSpace(only=['Rcs']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Rcs': 0.0094459606901065168}
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
Required Data
Full list of features
Parameters
Dependencies
Skew Extactor
Skew
The skewness of a sample is defined as follow:
\(Skewness = \frac{N}{(N-1)(N-2)} \sum_{i=1}^N (\frac{m_i-\hat{m}}{\sigma})^3\)Example:
For a normal distribution it should be equal to zero:
>>> fs = feets.FeatureSpace(only=['Skew']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Skew': -0.00023325826785278685}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
SlottedA_length Extactor
SlottedA_length - Slotted Autocorrelation
In slotted autocorrelation, time lags are defined as intervals or slots instead of single values. The slotted autocorrelation function at a certain time lag slot is computed by averaging the cross product between samples whose time differences fall in the given slot.
\(\hat{\rho}(\tau=kh) = \frac {1}{\hat{\rho}(0)\,N_\tau} \sum_{t_i}\sum_{t_j= t_i+(k-1/2)h }^{t_i+(k+1/2)h} \bar{y}_i(t_i)\,\, \bar{y}_j(t_j)\)Where \(h\) is the slot size, \(\bar{y}\) is the normalized magnitude, \(\hat{\rho}(0)\) is the slotted autocorrelation for the first lag, and \(N_\tau\) is the number of pairs that fall in the given slot.
>>> fs = feets.FeatureSpace( ... only=['SlottedA_length'], SlottedA_length={"t": 1}) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'SlottedA_length': 1.}Parameters
T: tau - slot size in days (default=1).
References
huijse2012information Huijse, P., Estevez, P. A., Protopapas, P., Zegers, P., & Principe, J. C. (2012). An information theoretic algorithm for finding periodicities in stellar light curves. IEEE Transactions on Signal Processing, 60(10), 5135-5145.
Required Data
Full list of features
Parameters
1
Dependencies
SmallKurtosis Extactor
SmallKurtosis
Small sample kurtosis of the magnitudes.
\(SmallKurtosis = \frac{N (N+1)}{(N-1)(N-2)(N-3)} \sum_{i=1}^N (\frac{m_i-\hat{m}}{\sigma})^4 - \frac{3( N-1 )^2}{(N-2) (N-3)}\)For a normal distribution, the small kurtosis should be zero:
>>> fs = feets.FeatureSpace(only=['SmallKurtosis']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'SmallKurtosis': 0.044451779515607193}See http://www.xycoon.com/peakedness_small_sample_test_1.htm
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
Std Extactor
Std - Standard deviation of the magnitudes
The standard deviation \(\sigma\) of the sample is defined as:
\(\sigma=\frac{1}{N-1}\sum_{i} (y_{i}-\hat{y})^2\)For example, a white noise time serie should have \(\sigma=1\)
>>> fs = feets.FeatureSpace(only=['Std']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'Std': 0.99320419310116881}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
StetsonJ Extactor
These three features are based on the Welch/Stetson variability index \(I\) (Stetson, 1996) defined by the equation:
\(I = \sqrt{\frac{1}{n(n-1)}} \sum_{i=1}^n { (\frac{b_i-\hat{b}}{\sigma_{b,i}}) (\frac{v_i - \hat{v}}{\sigma_{v,i}})}\)where :math:b_i and \(v_i\) are the apparent magnitudes obtained for the candidate star in two observations closely spaced in time on some occasion \(i\) , \(\sigma_{b, i}\) and \(\sigma_{v, i}\) are the standard errors of those magnitudes, \(\hat{b}\) and hat{v} are the weighted mean magnitudes in the two filters, and \(n\) is the number of observation pairs.
Since a given frame pair may include data from two filters which did not have equal numbers of observations overall, the "relative error" is calculated as follows:
\(\delta = \sqrt{\frac{n}{n-1}} \frac{v-\hat{v}}{\sigma_v}\)allowing all residuals to be compared on an equal basis.
StetsonJ
Stetson J is a robust version of the variability index. It is calculated based on two simultaneous light curves of a same star and is defined as:
\(J = \sum_{k=1}^n sgn(P_k) \sqrt{|P_k|}\)with \(P_k = \delta_{i_k} \delta_{j_k}\)
For a Gaussian magnitude distribution, J should take a value close to zero:
>>> fs = feets.FeatureSpace(only=['StetsonJ']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'StetsonJ': 0.010765631555204736}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
StetsonK Extactor
These three features are based on the Welch/Stetson variability index \(I\) (Stetson, 1996) defined by the equation:
\(I = \sqrt{\frac{1}{n(n-1)}} \sum_{i=1}^n { (\frac{b_i-\hat{b}}{\sigma_{b,i}}) (\frac{v_i - \hat{v}}{\sigma_{v,i}})}\)where :math:b_i and \(v_i\) are the apparent magnitudes obtained for the candidate star in two observations closely spaced in time on some occasion \(i\) , \(\sigma_{b, i}\) and \(\sigma_{v, i}\) are the standard errors of those magnitudes, \(\hat{b}\) and hat{v} are the weighted mean magnitudes in the two filters, and \(n\) is the number of observation pairs.
Since a given frame pair may include data from two filters which did not have equal numbers of observations overall, the "relative error" is calculated as follows:
\(\delta = \sqrt{\frac{n}{n-1}} \frac{v-\hat{v}}{\sigma_v}\)allowing all residuals to be compared on an equal basis.
StetsonK
Stetson K is a robust kurtosis measure:
\(\frac{1/N \sum_{i=1}^N |\delta_i|}{\sqrt{1/N \sum_{i=1}^N \delta_i^2}}\)where the index \(i\) runs over all \(N\) observations available for the star without regard to pairing. For a Gaussian magnitude distribution K should take a value close to \(\sqrt{2/\pi} = 0.798\) :
>>> fs = feets.FeatureSpace(only=['StetsonK']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'StetsonK': 0.79914938521401002}
References
richards2011machine Richards, J. W., Starr, D. L., Butler, N. R., Bloom, J. S., Brewer, J. M., Crellin-Quick, A., ... & Rischard, M. (2011). On machine-learned classification of variable stars with sparse and noisy time-series data. The Astrophysical Journal, 733(1), 10. Doi:10.1088/0004-637X/733/1/10.
Required Data
Full list of features
Parameters
Dependencies
StetsonKAC Extactor
These three features are based on the Welch/Stetson variability index \(I\) (Stetson, 1996) defined by the equation:
\(I = \sqrt{\frac{1}{n(n-1)}} \sum_{i=1}^n { (\frac{b_i-\hat{b}}{\sigma_{b,i}}) (\frac{v_i - \hat{v}}{\sigma_{v,i}})}\)where :math:b_i and \(v_i\) are the apparent magnitudes obtained for the candidate star in two observations closely spaced in time on some occasion \(i\) , \(\sigma_{b, i}\) and \(\sigma_{v, i}\) are the standard errors of those magnitudes, \(\hat{b}\) and hat{v} are the weighted mean magnitudes in the two filters, and \(n\) is the number of observation pairs.
Since a given frame pair may include data from two filters which did not have equal numbers of observations overall, the "relative error" is calculated as follows:
\(\delta = \sqrt{\frac{n}{n-1}} \frac{v-\hat{v}}{\sigma_v}\)allowing all residuals to be compared on an equal basis.
StetsonK_AC
Stetson K applied to the slotted autocorrelation function of the light-curve.
>>> fs = feets.FeatureSpace(only=['SlottedA_length','StetsonK_AC']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'SlottedA_length': 1.0, 'StetsonK_AC': 0.20917402545294403}Parameters
T: tau - slot size in days (default=1).
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
Required Data
Full list of features
Parameters
1
Dependencies
StetsonL Extactor
These three features are based on the Welch/Stetson variability index \(I\) (Stetson, 1996) defined by the equation:
\(I = \sqrt{\frac{1}{n(n-1)}} \sum_{i=1}^n { (\frac{b_i-\hat{b}}{\sigma_{b,i}}) (\frac{v_i - \hat{v}}{\sigma_{v,i}})}\)where :math:b_i and \(v_i\) are the apparent magnitudes obtained for the candidate star in two observations closely spaced in time on some occasion \(i\) , \(\sigma_{b, i}\) and \(\sigma_{v, i}\) are the standard errors of those magnitudes, \(\hat{b}\) and hat{v} are the weighted mean magnitudes in the two filters, and \(n\) is the number of observation pairs.
Since a given frame pair may include data from two filters which did not have equal numbers of observations overall, the "relative error" is calculated as follows:
\(\delta = \sqrt{\frac{n}{n-1}} \frac{v-\hat{v}}{\sigma_v}\)allowing all residuals to be compared on an equal basis.
StetsonL
Stetson L variability index describes the synchronous variability of different bands and is defined as:
\(L = \frac{JK}{0.798}\)Again, for a Gaussian magnitude distribution, L should take a value close to zero:
>>> fs = feets.FeatureSpace(only=['SlottedL']) >>> features, values = fs.extract(**lc_normal) >>> dict(zip(features, values)) {'StetsonL': 0.0085957106316273714}
References
kim2011quasi Kim, D. W., Protopapas, P., Byun, Y. I., Alcock, C., Khardon, R., & Trichas, M. (2011). Quasi-stellar object selection algorithm using time variability and machine learning: Selection of 1620 quasi-stellar object candidates from MACHO Large Magellanic Cloud database. The Astrophysical Journal, 735(2), 68. Doi:10.1088/0004-637X/735/2/68.
Required Data
Full list of features
Parameters
Dependencies
StructureFunctions Extactor
- The structure function of rotation measures (RMs) contains information
- on electron density and magnetic field fluctuations.
References
simonetti1984small Simonetti, J. H., Cordes, J. M., & Spangler, S. R. (1984). Small-scale variations in the galactic magnetic field-The rotation measure structure function and birefringence in interstellar scintillations. The Astrophysical Journal, 284, 126-134.
